
Many fans of Lego are aware of the geometry of the brick, such as the fact that a standard brick has a 5/6 width to height relationship. Much has been written about the height of five stacked plates being the exact width of two bricks. Understanding the geometry of the brick is an essential skill in advanced construction techniques. With that said, there seems to be little attention paid to the need to occasionally connect some creation or another on a diagonal line. This technique is arguably less useful than the aforementioned height / width relationship, but the following information may prove valuable to some.
When attempting to connect a length of brick (such as a wall, etc) in a diagonal orientation, it is useful to know where the studs will line up. Whether or not they’ll line up depends on the length of the hypotenuse (the long edge on a right triangle). If the hypotenuse happens to be the exact distance of any multiple of the width of a brick, the studs line up. The formula for determining the hypotenuse is the trusty old Pythagorean Theorem. Considering we’re always working with right triangles, we simply count the number of studs on the length and width axis. Subtract one from both length and width. Then use the following formula to determine if the particular point has a hypotenuse which lines up.
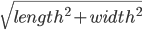
For example, the smallest point at which the studs all align for a clean diagonal fit using a standard baseplate grid is a rectangle with the dimensions of 4 x 5. A 6 stud length of brick closes the hypotenuse, as shown below. The calculation can be a bit confusing because the actual measurement to find the hypotenuse is taken from stud center to stud center, rather than the typical measurement from outside edge to outside edge, as seen in the figure to the right. 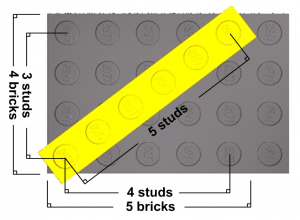
Carrying on the example in the figure, the length is 4 bricks and the width is 5 bricks. Subtract 1 from both to find the stud center to stud center length/width values (3 x 4). Then plug them into the equation above to arrive at:
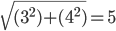
We end up with a hypotenuse of 5 studs. Again, measured stud center to stud center. With this knowledge in hand, we can set out to calculate the direct line length from the point of origin to any other point on the grid. While the task may be relatively simple, the scope can be a bit daunting. After all, on a standard 48 x 48 stud baseplate that would require running the calculation for 2209 possible points! That is why I’ve come up with this guide to show exactly where those points are on the 48 x 48 baseplate.
Here is a top-down view of a standard 48 x 48 baseplate with each possible connection point shown with a different color 1 x 1 round plate. The lower left corner is the initial point of origin. The plates that are the same color are on the same plane. That is, they’re simply another step using the same calculations as the previous step, but using the last connection point to represent a new point of origin.

The following table shows each of the possible connections (by color) and their dimensions. The first value in each box is the stud center to stud center measurement, while the value in parenthesis (the “Real” value) is the distance in bricks.
|
Length (Real) |
Width (Real) |
Hypotenuse (Real) |
 |
3 (4) |
4 (5) |
5 (6) |
 |
5 (6) |
12 (13) |
13 (14) |
 |
7 (8) |
24 (25) |
25 (26) |
 |
8 (9) |
15 (16) |
16 (17) |
 |
9 (10) |
40 (41) |
41 (42) |
 |
12 (13) |
35 (36) |
36 (37) |
 |
20 (21) |
21 (22) |
28 (29) |
 |
28 (29) |
45 (46) |
53 (54) |












